Chapter 7 Quantifying uncertainty

7.1 Sources of uncertainty

Nearly every DALY estimation is subject to data uncertainty and modelling choices. The resulting DALY estimate is thus hardly ever a single, fixed value, defined with perfect accuracy and precision. In a practical guide on accounting for uncertainty in decision-analytic models, Bilcke et al. (2011) classified uncertainty into three categories: parameter uncertainty (uncertainty regarding the true value of the model parameters); structural or model uncertainty (uncertainty regarding the model structure); and methodological uncertainty (uncertainty due to normative or subjective modelling choices).

7.1.1 Parameter uncertainty

Parameter uncertainty relates to a lack of knowledge on the true value of model parameters. DALY calculations require demographic, epidemiological, and severity parameters, each of which can be uncertain. Severity parameters, such as duration and disability weight, relate to individual patients and can therefore also be variable. Variability, sometimes referred to as stochasticity or first order uncertainty, distinguishes itself from uncertainty in that it is an inherent property of populations, and cannot be reduced by gaining more information, e.g., by increasing the sample size.

In general, parameter uncertainty results from sampling error and/or systematic error or bias. Sampling error is well known and well-studied by statisticians. It arises when a parameter is inferred from a representative sample of the population of interest. It can be modelled directly, for instance by assuming a Binomial distribution for a prevalence estimate obtained by testing a certain population sample. At a different level, when parameters are modelled from a statistical model, the resulting standard errors also reflect this sampling error. Systematic error, on the other hand, is less well-studied, but is potentially much more important. In DALY calculations, systematic error is very often related to the extrapolation of parameter values from non-representative populations or time periods. The most extreme form of extrapolation occurs when there is a complete lack of data, a common situation in global or regional burden of disease studies. It is not clear to what extent these alternative settings are representative for the concerned setting, and different alternative settings may provide different parameter values, related to different levels of bias. Ill-defined coding, misclassification and underestimation are typical and common sources of systematic error in epidemiological parameters such as prevalence, incidence and mortality (see section 3.1).

A specific problem related to parameter uncertainty arises when uncertainty is correlated. This may be the case if DALYs are calculated per age and sex group, but parameters are only available at a less granular level. In GBD studies, this problem occurs when regional or global parameters are used instead of country-specific parameters and applied to each of the concerned countries. Such issues may be described as stratification uncertainty: uncertainty arising because the level of detail required in the DALY calculations does not match the level of stratification in the data (Devleesschauwer et al., 2016).

7.1.2 Model uncertainty

DALY calculations follow a disease model or outcome tree, i.e., a schematic representation of health states that are causally related to the risk factor, hazard or disease of interest (Devleesschauwer et al., 2014c). Uncertainty in this disease model may arise when there is insufficient or conflicting evidence on the causal relation of certain symptoms. Such uncertainty is common for long-term outcomes of infections, such as cirrhosis and hepatocellular carcinoma following hepatitis C and B infection (García-Fulgueiras et al., 2011), or post-infectious irritable bowel syndrome following giardiosis (Havelaar et al., 2012). Model uncertainty in DALY calculations may also originate from health states being controversial due to ethical reservations. In this respect, Jamison et al. (2006) discussed the inclusion of stillbirths in GBD assessments.

A second source of model uncertainty can be linked to the epidemiological data used in the DALY calculations. Often the available data come with a lot of restrictions, and several assumptions need to be made to transform these into useable numbers. Whether or not data should be corrected for underreporting or misclassification may for instance become a source of model uncertainty.

7.1.3 Methodological uncertainty

The DALY metric encapsulates various methodological choices, often referred to as value choices. All of these choices are normative and thus subjective, as there is no intrinsically correct choice. As a result, different choices are being made, and contested, in literature.

The different methodological choices that need to be made when calculating DALYs have been outlined in section 2 of the manual. Here we provide some examples of how these choices can lead to uncertainties.

1. YLD perspective

The GBD 2010 study introduced a prevalence-based version of the YLD, defined as the product of number of prevalent cases and DW (Murray et al., 2012). Both perspectives are equally valid, but have a different interpretation. The choice between an incidence and prevalence perspective therefore remains a normative choice.

2. Disability weights

Different methods exist for deriving DWs, based on either an econometric or psychometric philosophical perspective on health-related quality of life (Haagsma et al., 2014; Rehm and Frick, 2010). Also, subjective choices need to be made on which population’s values to use: those of patients, lay people, or disease experts? Phanthunane et al. (2010) for instance compared DWs for schizophrenia elicited from both patients and clinicians using different multi-attribute utility instruments. Furthermore, DWs may be corrected for comorbidity, but again, different methods have been proposed, ranging from the use of arbitrary attribution factors (Mathers et al., 2000), over maximum limit or multiplicative approaches (Mathers et al., 2001; Murray et al., 2012), to regression models (Cuijpers et al., 2011; Lokkerbol et al., 2013). Finally, when DWs are not available for specific health states, “proxy” DWs are commonly derived by mapping the concerned health state to alternative health states for which DWs are available. LaBeaud et al. (2011) for instance present a set of proxy DWs for arbovirus-related long-term sequelae, showing the uncertainty induced by the need to map to analogous health states.

3. Residual life expectancy table

Different possibilities exist regarding the choice of the life expectancy table. The use of local (e.g., national) life expectancy tables has been propagated to reflect the local epidemiological situation (Plass et al., 2013). Local life expectancy tables have also been used for specific population subgroups, such as ethnic minorities in Australia (Costilla et al., 2013), or for future populations, such as the French population in 2020 (Lapostolle et al., 2008). Some authors further adapted local life expectancies to reflect reduced life expectancy in fatal cases, assuming that these cases had underlying diseases (Wielders et al., 2012). Matemba et al. (2010) used the opposite approach, by adapting the local life expectancy table to estimate the burden of sleeping sickness if the HIV/aids epidemic had not occurred. In addition to these local life expectancy tables, the use of so-called “standard” life expectancy tables has been promoted to ensure comparability across populations. To date, however, there are three different “standard” life expectancy tables in use (Appendix A).

4. Social weighting

The basic DALY formulas can be extended by including age weighting and time discounting functions (Devleesschauwer et al., 2014b). Whether or not these social weighting functions should be used remains a subjective choice, and has indeed been the subject of debate (Barendregt et al., 1996). Furthermore, there is no consensus on the exact parameterization of these social weighting functions. Although age weighting commonly follows the original formulation, some authors proposed alternative formulations that better reflected their local situation (Yang et al., 2004). When discounting time, the standard choice has been to apply a 3% discount rate, but certain national instances propose different weights, e.g., 1.5% in The Netherlands and 3.5% in the United Kingdom (Havelaar et al., 2012).

7.2 Dealing with uncertainties

7.2.1 Probabilistic sensitivity analysis

By far the most powerful method to deal with parameter uncertainty is probabilistic sensitivity analysis (PSA), sometimes also called uncertainty analysis or uncertainty propagation. In PSA, the uncertain parameters are represented by uncertainty distributions, thereby following the Bayesian definition of probability as a degree of belief instead of a long-term frequency. PSA uses Monte Carlo simulations, or parametric bootstrap, to sample random values from the specified uncertainty distributions (Fig 7). At each iteration, the sampled values are used to calculated a DALY estimate. The combination of iterations therefore results in an empirical distribution of DALY estimates, reflecting the joint uncertainty in the input parameters (Fig 8). This resulting distribution can be summarized by its mean and a 95% uncertainty interval defined as the 2.5th and 97.5th percentile. PSA is typically used to propagate uncertainty, thereby ignoring variability. Nevertheless, it would be possible to simulate both processes using second order or two-dimensional Monte Carlo simulations (Havelaar et al., 2004).

Fig 7. Monte Carlo simulation. Top: red dots represent seven simulated values from a normal(0;1) distribution. Bottom: as the number of Monte Carlo simulations increases, the histogram of simulated values becomes an increasingly better approximation of the target distribution (in blue).

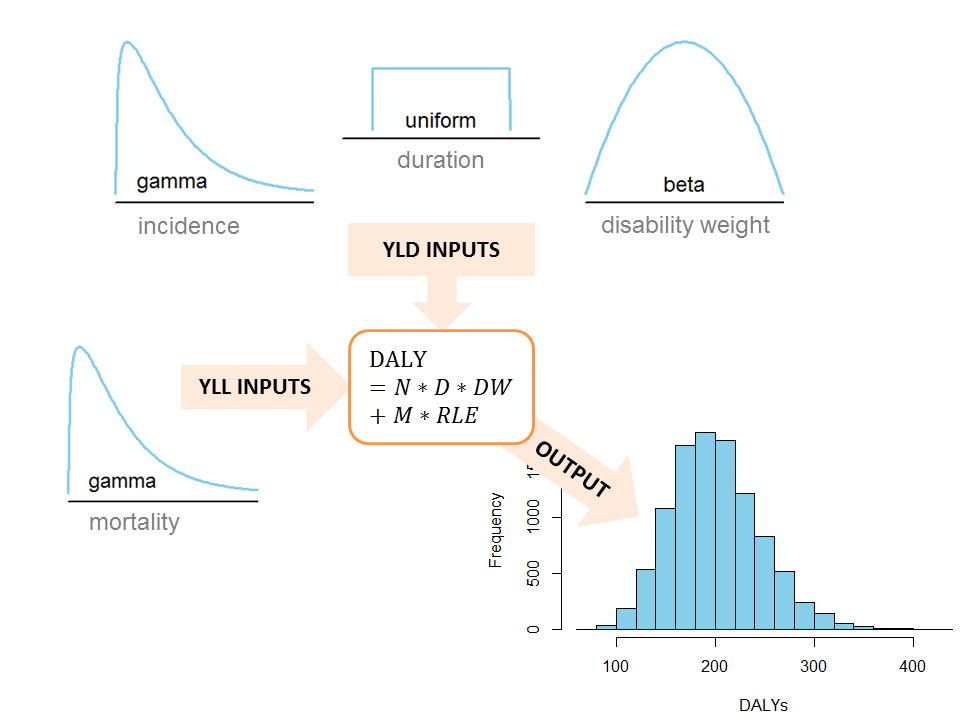
Probabilistic sensitivity analysis applied to DALY calculations. Probability distributions are specified to reflect the uncertainty in the input parameters; random values are simulated from these distributions and used to calculate DALYs, resulting in an empirical distribution of the joint uncertainty in the DALY estimate.

7.2.2 Variable importance analysis

To evaluate which uncertain parameters contribute most to the uncertainty in the final DALY estimate, variable importance analysis techniques can be applied. These techniques are often also called sensitivity analyses, adding to the confusion. A common approach is to calculate standardized regression coefficients, by regressing the standardized input parameters against the (standardized) simulated DALYs obtained with PSA (Verhoef et al., 2012). The resulting regression coefficients reflect the expected (standard deviation) change in DALY per standard deviation change in the respective input parameter. Alternatively, partial correlation coefficients may be calculated, which do not assume a linear relationship between inputs and output. For both methods, the resulting variable importance coefficients may be represented in a tornado graph, which sorts, from top to bottom, the input variables in order of their importance (Fig 9).

Fig 9. Tornado graph showing the results of a variable importance analysis in a study on the burden of neurocysticercosis-epilepsy in Tanzania (Trevisan et al. 2016). E: epilepsy; NCC: neurocysticercosis.

7.2.3 Scenario analyses

Scenario analyses imply that DALYs are calculated under different assumptions and compared. These analyses are the method of choice for quantifying model and methodological uncertainty. Fig 10 shows an example.

Fig 10. Scenario analysis of the disease burden of toxoplasmosis in the Netherlands (Havelaar et al., 2007). The evaluated scenarios include alternative incidence data, the inclusion of time discounting, the exclusion of fetal losses, and the use of alternative disability weights

In theory, model and methodological uncertainty may also be assessed through PSA, by parameterizing the uncertain model elements or the methodological choices. Whether or not underreporting should be corrected for, could for instance be parameterized by specifying an uncertainty distribution on the underreporting factor with a minimum of one and a certain maximum. Indeed, Luz et al. (2009) performed a PSA with a multiplication factor ranging from 0.3 to 10, thus accounting for over-reporting, over correct reporting, to underreporting, with a stronger emphasis on the former. Including or excluding a certain health state could for instance be modelled as a Bernoulli random variable with inclusion probability π. The resulting distribution of simulated DALY estimates will then be a combination of different disease model assumptions, which in itself can be regarded as a new scenario. Furthermore, parameterization would prevent decision makers to identify the results that correspond to their model choice or methodological preference.